CNN과 이미지가 찰떡궁합인 이유
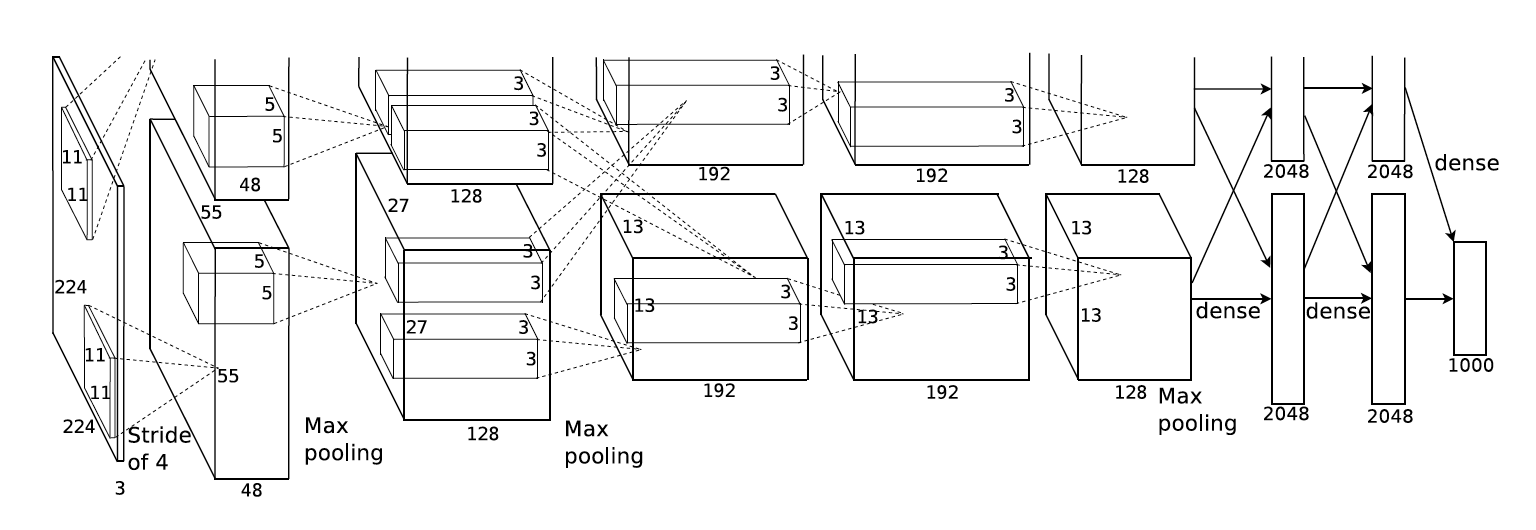
딥러닝이 뜨고 지금까지 가장 활약한 모델 중 하나는 CNN이다. 대부분의 사람들이 아무런 의심없이 이미지 데이터를 다룰때는 CNN을 사용한다. 그렇다면 도데체 왜 CNN은 이미지 데이터를 잘 처리하는 것일까? 그 근본적인 이유에 대해 알아보자.
머신러닝의 가정
머신러닝(딥러닝) 모델들은 저마다 어떤 가정하에서 만들어진다. 모델들마다 “나는 이런 특성을 가진 데이터를 주로 다루겠다.” 라고 선을 긋는 것이다. 그래서 각 모델의 가정을 잘 아는것과 데이터 특성에 맞는 모델을 잘 선택하는 것이 중요하다.
CNN의 가정
Alexnet 논문을 보면 이미지가 가진 특성에 대한 CNN의 가정이 짧게 언급된다.
“They also make strong and mostly correct assumptions about the nature of images (namely, stationarity of statistics and locality of pixel dependencies).”
바로 stationarity of statistics와 locality of pixel dependencies이다. 짧게 stationarity, locality라고 하겠다. stationarity는 시계열 데이터의 통계적인 특성이 시간이 지나도 변하지 않는다는 뜻이고, locality는 이미지에서 한 점과 의미있게 연결된 점들은 주변에 있는 점들로만 국한된다는 뜻이다.
Stationarity
stationarity는 확률론에서 시계열의 통계적 속성이 시간에 관계없이 변하지 않은것을 의미한다. 쉽게 말해 시간이 변해도 동일한 패턴이 반복된다는 뜻이다. 당연하게도 동일한 패턴이 반복되면 분석도 훨씬 쉬워진다.

이미지는 시간 대신 위치에 관계없이 동일한 패턴들이 반복되는 특징을 가지고 있다. 그렇기 때문에 stationarity 가정하에 시계열과 비슷하게 이미지의 패턴을 파악할 수 있다.
즉 이미지의 특정 위치에서 학습한 파라미터를 이용해서 다른 위치에 있는 동일한 특징을 추출할 수 있다는 뜻이다.
아래 사진을 보면 두 명의 입이 서로 다른 위치에 존재한다. 물론 입 모양이 많이 다르고 좀 극단적이긴 하지만 이것이 이미지의 stationarity가정으로 위치에 관계없이 발견될 수 있는 동일한 패턴으로 볼 수 있겠다.

convolution
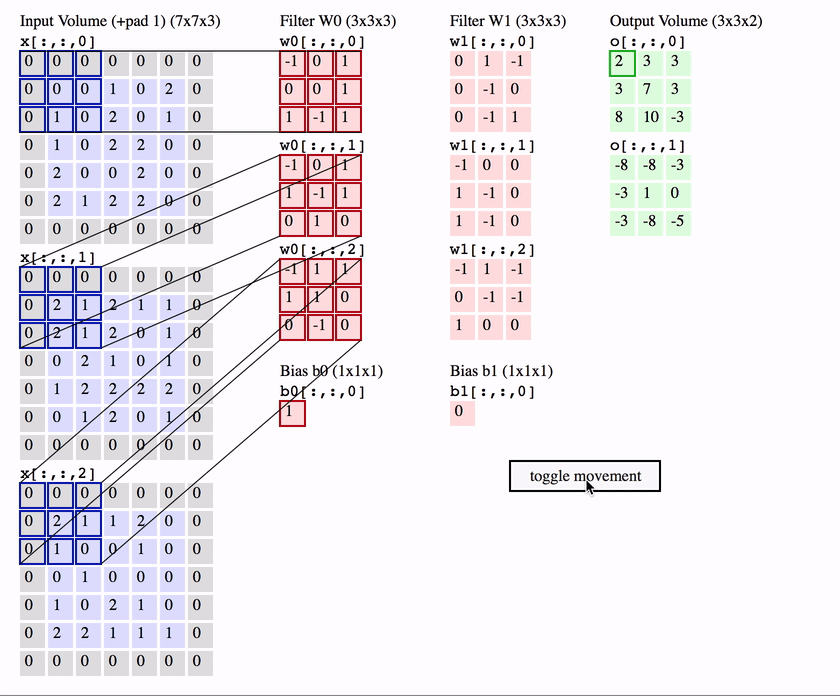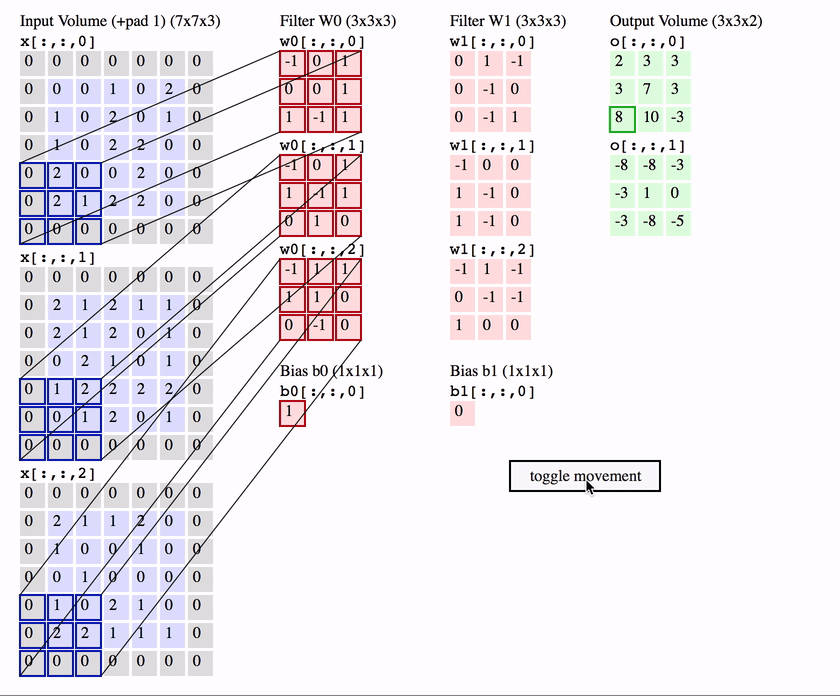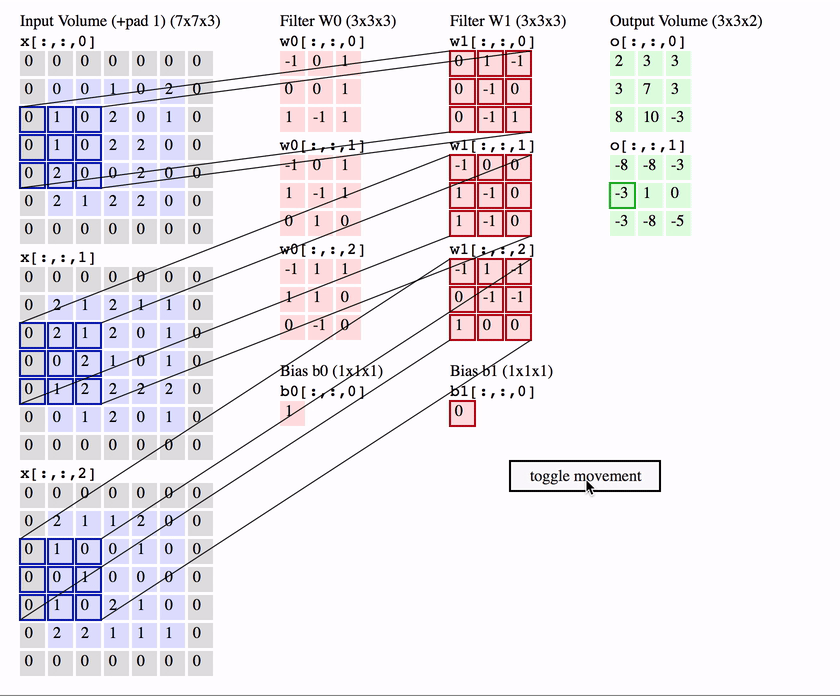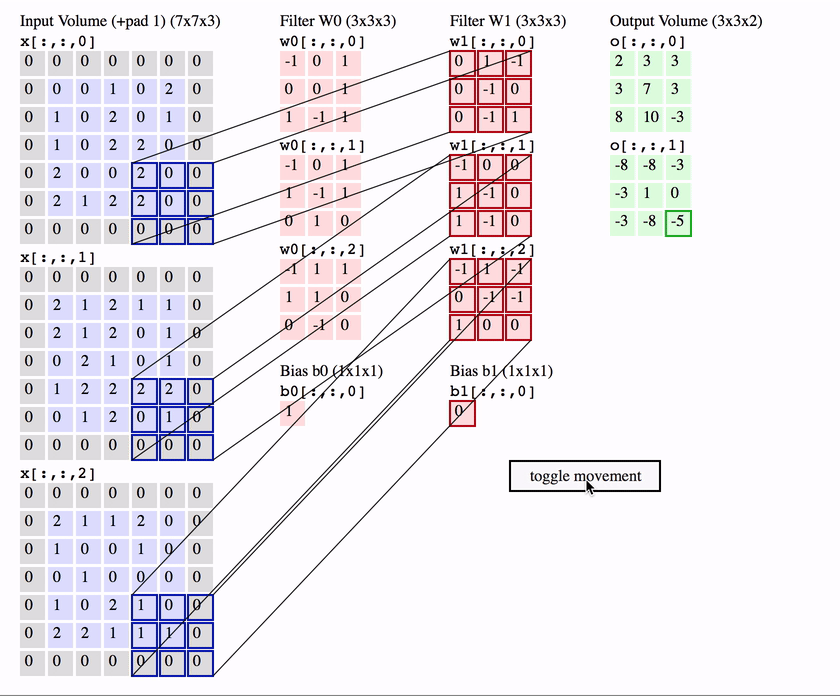
딥러닝부터 공부한 사람들은(필자처럼) 보통 Convolution 연산을 CNN의 가장 핵심이 되는 연산으로 시작한걸로 알고 있지만 오래전부터 시계열 데이터를 다루는 신호처리에서 1-convolution을 널리 사용하였고 사실 이미지도 영상신호이기 때문에 2-d convolution을 사용하는것 뿐이다.

Convolution은 입력함수(입력)와 대상함수를 연산하여 출력함수를(출력) 계산하는 연산이다. 위 그림처럼 붉은 대상함수를 반전하여 입력함수 위를 이동하면서 곱한 다음, 구간에 대해 적분하여 출력함수를 계산한다.
이미지를 입력함수로 보고, 필터를 대상함수로 보면 이미지위에 작은 필터를 이동시키면서 각 위치의 이미지 영역과 필터를 Convoultion하여 feature map을 출력하는 것이다.
이 Convolution연산은 이미지의 특정 부분과 필터를 내적하는것으로 볼 수도 일다. 두 벡터가 유사할수록 큰 값을 출력하는 내적의 특성에 의해 필터는 이미지에 있는 패턴들과 유사한 형태로 학습이 되는것이다.
많은 머신러닝 프레임워크에서는 필터를 반전하는 것을 제외하고는 Convolution과 완전 동일한 연산인 Cross-correlation을 구현한다. CNN에서 Convolution연산은 특징만 학습하면 되기 때문에 필터를 반전시키지 않아도 동일한 효과를 낼 수 있다.
parameter sharing
위 사진에서 입이라는 특징을 뽑아낸다고 할 때 두 가지 방법이 있다.
- 2개의 입을 하나의 특징으로 취급하여 위치와 상관없이 입 2개를 추출하는것과
- 위치를 고려하여 서로 다른 특징 2개를 추출하는 것(특징1-왼쪽에 위치한 입, 특징2-오른쪽에 위치한 입)
2가지 방법 중 어떤 것이 더 효율적일까?
당연히 전자가 더 효율적이며 파라미터를 공유하는 이유가 바로 위치에 상관없이 특징을 추출하기 위해서다. 후자는 동일한 특징이라도 위치가 다르면 다른 특징으로 인식해야 해서 위치마다 모두 다른 필터를 사용해야 하기 때문에 엄청나게 비효율적일 수 밖에 없다.
파라미터 공유는 feature map 하나를 출력하기 위해 필터를 단 한장만 유지하기 때문에 full-connected layer보다 훨씬 적은 파라미터 수를 사용하여 메모리를 아끼고 연산량도 적어지고 statistical efficiency 또한 향상된다.
statistical efficiency란, 예측 모델의 품질 측정방법으로 더욱 효율적인 모델은 상대적으로 데이터 수를 적게 학습시켜도 더 좋은 성능을 내야한다는 의미다.
파라미터 공유덕분에 한장의 feature map을 만드는데 동일한 특징을 여러곳에서 볼 수 있기 때문에 fc 레이어에 비해 동일한 학습 데이터셋 상황에서도 더 많은 데이터를 학습한 효과를 갖게 되고 결국 statistical efficiency가 향상된다.
아래 그림은 파라미터 공유를 설명하는 2가지 예제다.


stationarity & convolution
드디어 stationarity가정으로 convolution연산을 사용하는 이유를 설명할 수 있게 되었다.
이미 눈치채신 분들도 있겠지만 위에서 설명한 stationarity는 이미지 위치에 상관없이 동일한 특징들이 존재한다는 가정이기 때문에 파라미터를 공유(Parameter sharing)하는 Convolution 연산과 아주 잘 어울린다.
입이라는 특징을 학습한 필터 하나가 이미지 전체 영역을 이동하면서(parameter sharing) Convolution 연산을 수행하면 stationarity 특성을 가진 이미지에서 한장의 입 모양 필터로 여러개의 입 특징을 모두 추출할 수 있게 된다.
이렇게 stationarity 특성을 잘 살리면서 비교적 연산량은 더 적고, 메모리 사용량도 적고, 통계적 효율성도 더 높기 때문에 CNN이 이미지 데이터를 잘 다를 수 밖에 없다고 생각된다.
translation equivariance
또 다른 시각으로 해석해보자. convolution 연산은 translation equivariance 특성을 가지고 있다.
equivariance란 쉽게 말하면 함수의 입력이 바뀌면 출력 또한 바뀐다는 뜻이고, translation equivariance는 입력의 위치가 변하면 출력도 동일하게 위치가 변한채로 나온다는 뜻이다.
그래서 convolution연산을 하면 translation equivariance 특성과 더불어 파라미터를 공유하기때문에 필터 하나로 다양한 위치에서 특징들을 추출할 수 있게 되고 결국 이미지의 stationarity 가정과 찰떡 궁합이라고 말할 수 있겠다.
translation equivariance vs translation invariance

equivariance와 invariance는 서로 반대되는 개념이다. invariance는 불변성이라는 뜻으로 함수의 입력이 바뀌어도 출력은 그대로 유지되어 바뀌지 않는 다는 뜻이다.
고로 translation invariance는 입력의 위치가 변해도 출력은 변하지 않는다는 의미로 강아지 사진에 강아지가 어느 위치에 있건 상관없이 그냥 강아지라는 출력을 한다는 의미다.
(max-pooing은 대표적인 small translation invariance 함수이다. 여러 픽셀 중 최대값을 가진 픽셀 하나를 출력하기 때문에 서로 다른 [1,0,0], [0,0,1] 두 입력을 넣어도 동일한 1을 출력하게 된다. 그래서 입 모양이 약간씩 다르거나 위치가 조금씩 다른 경우에도 동일한 입으로 인식하게 되는 것이다.)
여기서 중요한건 CNN모델이 convolution연산의 equivariance 특성에 파라미터 공유를 더하게 되면 나오는 결과이다. convolution + 파라미터 공유를 하면 equivariance를 통해 반대 특성인 translation invariance 특성 또한 갖게 된다.
파라미터를 공유하지 않으면 위치마다 다른 필터를 사용하기 때문에 하단에 있는 토끼 이미지만 학습했다면 상단의 있는 토끼 이미지의 경우 처음보는 특성으로 판단하여 토끼라고 판단하지 않을 수 있다. 즉 translation invariance특성을 갖지 못하게 된다는 것이다.
아래 그림은 translation equivariance가 translation invariance하게 바뀌는 가정을 표현하고 있다.
CNN자체를 label의 확률을 출력하는 하나의 커다란 합성 함수로 보자. 그 안에 포함된 Convolution연산은 equivariant해서 서로 다른 위치에 있는 특징을 입력으로 넣으면 feature map에서도 각 특징을 서로 다른 위치에 배치시킨다. 즉 여기까지는 아직 invariant하지 않다는 뜻이다.
하지만 conv 레이어들을 지나서 fc레이어와 softmax를 거친 결과는 특징의 위치와는 상관없이 무조건 특징이 포함된 라벨의 확률 값을 높게 출력한다.
즉, 강아지 사진에 강아지가 어느 위치에 있건 강아지 label 확률값은 동일하게 높게 출력하기 때문에 Convolution연산의 equivariance한 특성과 파라미터 를 공유하는 덕분에 CNN자체가 translation invariant특성을 갖게 된다.
translation invariance가 싫어요
translation invariance를 피하고 싶은 경우도 있을까?
물론이다. 각 특징들의 위치 정보가 중요한 경우 translation invariance를 막는 CNN 아키텍쳐들도 있다.
예를 들어 정면으로 정중앙에 얼굴만 있는 사진을 학습할 때 눈이 아래에 있으면 얼굴로 판단하면 안된다.
이러한 경우를 위해 Locally connected layers(unshared convolution)는 일반적인 Convolution 연산과 동일하지만 파라미터 공유를 하지 않는다. 즉 각 위치마다 다른 필터를 사용하기 때문에 동일한 특징이라도 위치에 따라 다른 필터를 학습을 하게 된다.
결국 필터가 위치 정보를 포함한다고 볼 수 있으며, 결과적으로 translation invariance를 버리게 된다.(max-pooling을 사용한다면 small translation invariance 특성은 가질 수 있다.)
또 다른 유명한 모델로 캡슐 네트워크가 있다. 캡슐 네트워크는 아예 새로운 방식으로 translation invariance문제를 해결한다.
아래 그림은 캡슐 네트워크 포스팅에서 가장 많이 나오는 그림으로 CNN의 translation invariance 단점을 꼬집은 경우다. 오른쪽 그림은 얼굴이라고 볼 수 없는 사진이지만 위치에 상관없이 얼굴의 부분적인 특징들이 모두 있기 때문에 얼굴이라고 잘못 판단한다는 예제이다.

하지만 저 예제는 극단적으로 오버된 케이스다. 실제로 일반적인 CNN을 사용해도 오른쪽을 얼굴이라고 판단할 확률은 더 적다. 왜냐하면 깊은 Convolutional 레이어일수록 더 큰 형태의 특징들을 뽑아내기 때문에 저렇게 정확하게 눈, 코, 입 단위로만 따로 특징을 배워서 어떤 판단을 하지 않는다.
그리고 어느정도 전체 형태를 보기 때문에 각각의 작은 특징들의 위치를 아예 무시하지는 않는다는 뜻이다.
즉 CNN의 구조를 어떻게 만드느냐에 따라 저런 케이스정도는 충분히 커버가 가능하다는 말이다.
locality of pixel dependencies
locality of pixel dependencies는 쉽게 이미지는 작은 특징들로 구성되어 있기 때문에 픽셀의 종속성은 특징이 있는 작은 지역으로 한정된다는 의미이다.
아래 사진을 보면 코라는 특징은 파란색 사각형 안에 있는 픽셀값에서만 표현되고 해당 픽셀들끼리만 관계를 가진다고 볼 수 있다. 빨간색 사각형안의 픽셀들은 파란색 사각형안의 픽셀들과는 종속성이 없다.
즉 이미지를 구성하는 특징들은 이미지 전체가 아닌 일부 지역에 근접한 픽셀들로만 구성되고 근접한 픽셀들끼리만 종속성을 가진다는 가정이다.

이러한 가정은 CNN이 Sparse interactions특성을 갖는 필터로 Convolution연산을 하는것과 아주 잘 어울린다.
Sparse interactions는 하나의 출력 유닛이 입력의 전체 유닛과 연결되어 있지않고 입력의 일부 유닛들과만 연결되어 있다는 의미로 주변 픽셀들과만 연관이 있다는 가정인 locality와 딱 들어 맞는다.
(사실 첫번째 가정인 stationarity 또한 Sparse interactions방식과 잘 어울리지만 locality와 더 밀접하다고 생각되서 stationarity에서는 sparse interactions에 대한 언급을 하지 않았다.)
결론
이미지의 특성인 stationarity of statistics와 locality of pixel dependencies를 가정하여 만들어진 CNN 모델이 이미지를 잘 다루는 건 당연한 일이다.
동일한 특징이 이미지내 여러 지역에 있을 수 있고, 작은 지역안에 픽셀 종속성이 있다는 가정 때문에 파라미터를 공유하고 sparse interaction을 가지는 필터와 Convolution연산을 하는것은 완벽하게 잘 들어맞는다.
그리고 Convolution 연산의 translation equivariance 특성에 파라미터 공유를 더해서 CNN 이 translation invariance를 가지게 된다는 것도 이해했다.